Introduction

van Zadelhoff et al. 2002 present two spherically symmetric benchmark models for non-LTE line radiative transfer, each defined at two different density levels. This yields a total of four distinct problems, called 1a/1b and 2a/2b. The authors provide and compare numerical solutions calculated by several radiative transfer codes for each of these setups.

References and downloads

Publication	van Zadelhoff et al. 2002 [ADS]
Problem 1 ski files	zadel1a.ski zadel1b.ski
Problem 2 ski files	zadel2a.ski zadel2b.ski
Problem 2 input files	zadel2_import.txt zadel2_mesh.txt zadel2_wldistribution.txt zadel2_wlgrid.txt

Problem 1

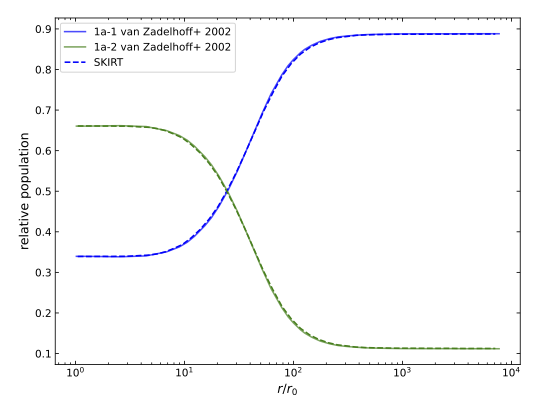
The first problem uses a fictional two-level molecule and a static sphere embedded in present-day cosmic microwave background radiation. The sphere has a power-law hydrogen number density, constant relative abundance of the test molecule, and constant gas temperature.

The figures below show the relative populations for each of the two energy levels as a function of radius for two different abundances: problem 1a (left) is a simple case with a moderate optical depth ( \(\tau\approx60\) from origin to infinity at line center), while problem 1b (right) has much higher optical depth ( \(\tau\approx4800\) ) and is therefore numerically stiffer. The SKIRT results (dashed lines) match the solutions presented by van Zadelhoff et al. 2002 (solid lines) very well.

To perform this benchmark, download the ski files zadel1a.ski and zadel1b.ski provided above (References and downloads). Then pass the (name of) each ski file to SKIRT as a single command line argument. At the end of the simulation run, SKIRT outputs level populations and line profiles for the emerging radiation which can be compared to the original benchmark results.

Problem 2

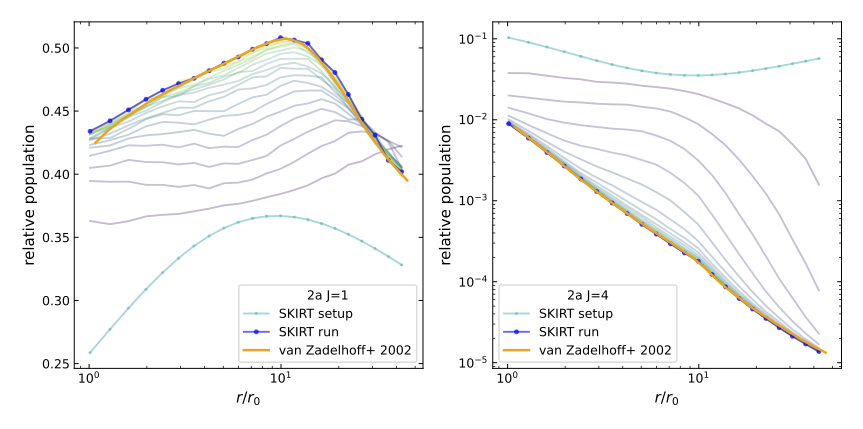
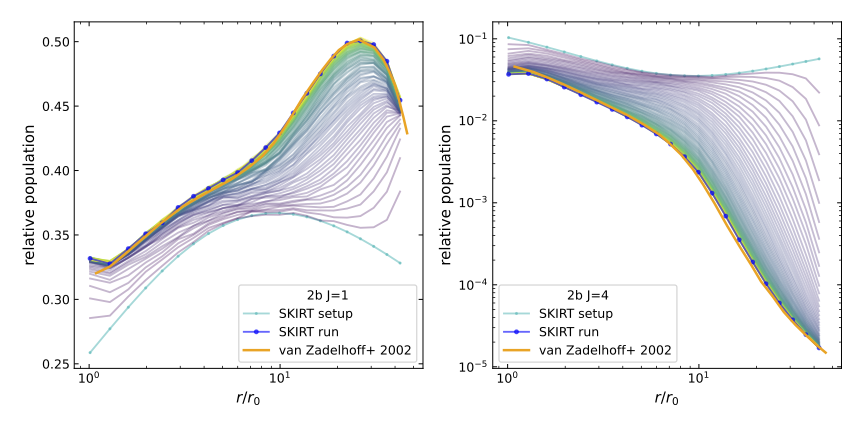
The second problem handles the formyl cation HCO+ in a collapsing sphere. The structure of the spherical cloud as a function of radius is taken from a dynamical simulation snapshot, including density, temperature, inward velocity, and local turbulent velocity. Similar to the first problem, the sphere is embedded in present-day cosmic microwave background radiation.

The figures below show the relative populations for the J=1 (left) and J=4 (right) energy levels as a function of radius for two different abundances (2a at the top and 2b at the bottom). The mean solution obtained by the various codes discussed by van Zadelhoff et al. 2002 is presented as the solid orange line. The converged SKIRT solution is shown in blue, with a dot at the center of each grid cell. The solutions match very well except for small discrepancies at the center of the sphere, which may be caused by gridding effects.

The cyan curve (with dots) traces the initial equilibrium conditions used for the calculation, and the weakly colored curves in between indicate the intermediate solutions after each iteration step in the calculation.

The current implementation of SKIRT requires a three-dimensional spatial grid for models that include kinematics. We therefore constructed import files for SKIRT that define the medium properties of the problem 2 sphere on a 3D Cartesian grid. This obviously increases the simulation runtime compared to a 1D model. This won't be an issue for more realistic models because they will likely have a 3D structure to begin with.

To perform this benchmark, download the ski files and the input files provided above (References and downloads). Then pass the (name of) the ski file to SKIRT as a single command line argument. At the end of the simulation run, SKIRT outputs level populations and line profiles for the emerging radiation which can be compared to the original benchmark results. It also outputs information about the level populations and the radiation field after every iteration step.