Material mixes (dust, electrons, gas)

This page offers an overview of material mix classes and their important properties. The discussion is organized as follows:

• Introduction
• The MaterialMix class hierarchy
• Single representative grain dust mixes
• Multiple grain population dust mixes
• Electrons
• Gas

Introduction

The transfer medium in a SKIRT simulation is represented by one or more medium components. For each component, the spatial density distribution can be specified through built-in geometries (GeometricMedium) or imported from input files (ImportedMedium). In either case, the optical properties of the medium are defined by associating a material mix (a MaterialMix subclass) with the medium component. The MaterialMix class hierarchy allows fundamentally different material types including dust, electrons, and gas to be implemented as part of a single framework.

For each spatial cell in the simulation, the medium state includes a number density value defining the amount of material present in the cell per unit of volume. The kind of physical entity being counted by the number density and the conversion from number density to mass density depend on the type of material, as indicated in the table below. The actual conversion factor is supplied by the material mix and obviously depends on the specific material type.

Material type	Entity counted	Mass conversion
Dust	hydrogen atom	dust mass per hydrogen atom
Electrons	electron	electron mass
Gas	hydrogen atom	gas mass per hydrogen atom

Most importantly, each MaterialMix subclass offers a set of functions that help implement the photon life cycle. For example, the MaterialMix::opacityAbs() and MaterialMix::opacitySca() functions return the absorption and scattering opacity given the incoming photon packet and the medium state in the spatial cell being crossed. The MaterialMix::performScattering() function handles a random-walk scattering interaction including the effects of bulk velocity, polarization, and so forth. The peelOffScattering() function similarly calculates the contribution to a scattering peel-off event given the instrument reference frame.

Furthermore, when applicable, a MaterialMix subclass also offers functions to help emit secondary photon packets. For example, the MaterialMix::emissionSpectrum() function returns the emission spectrum given the medium state in a cell and the radiation field in which the cell is embedded. Similarly, if the emission spectrum includes lines, the MaterialMix::lineEmissionSpectrum() function returns the luminosities that will be emitted at the line centers.

The following table lists some relevant physical quantities including properties that may be stored in the medium state or in a photon packet, material properties defined by material mixes, and properties that can be derived from these.

Symbol	Units	Description
$\lambda$	$\text{m}$	Wavelength
$\mathbf{r}$	$\text{m}$	Position
$\mathrm{\Delta }s$	$\text{m}$	Distance along a path
$a$	$\text{m}$	Dust grain size (radius)
$V$	${\text{m}}^3$	Volume
$\mathbf{v}$	$\text{m}{\text{s}}^{-1}$	Bulk velocity
$\mathbf{B}$	$\text{T}$	Magnetic field vector
$T$	$\text{K}$	Temperature
$n$	$\mathrm{\#}{\text{m}}^{-3}$	Number density (of entities)
$\mu$	$\text{kg}{\mathrm{\#}}^{-1}$	Mass per entity
$\varsigma$	${\text{m}}^2{\mathrm{\#}}^{-1}$	Cross section per entity
$\mathcal{N}=n\mathrm{\Delta }s$	$\mathrm{\#}{\text{m}}^{-2}$	Number column density
$N=nV$	$\mathrm{\#}$	Number (of entities)
$\rho =n\mu$	$\text{kg}{\text{m}}^{-3}$	Mass density
$\mathrm{\Sigma }=n\mu \mathrm{\Delta }s$	$\text{kg}{\text{m}}^{-2}$	Mass column density
$M=n\mu V$	$\text{kg}$	Mass
$\kappa =\varsigma /\mu$	${\text{m}}^2{\text{kg}}^{-1}$	Mass coefficient
$k=n\varsigma$	${\text{m}}^{-1}$	Opacity
$\tau =n\varsigma \mathrm{\Delta }s$	$1$	Optical depth

The MaterialMix class hierarchy

The diagram below shows a selection of the MaterialMix subclasses organized into logical groups. The precise class inheritance tree is slightly more complicated for practical implementation reasons.

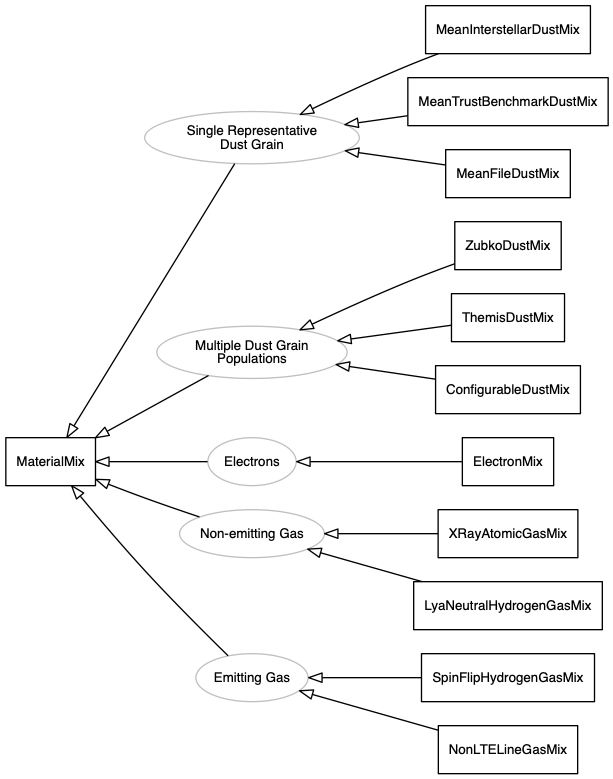
The sections below discuss each of these groups.

Single representative grain dust mixes

The abstract DustMix class inherits MaterialMix and implements the common functionality for all dust grain mixtures supported by SKIRT. Specifically, it handles the following basic dust material properties:

• the mass per entity $\mu$
• the absorption cross section per entity ${\varsigma }_{\lambda }^{\text{abs}}$
• the scattering cross section per entity ${\varsigma }_{\lambda }^{\text{sca}}$
• the total extinction cross section per entity ${\varsigma }_{\lambda }^{\text{ext}}={\varsigma }_{\lambda }^{\text{abs}}+{\varsigma }_{\lambda }^{\text{sca}}$
• the scattering albedo ${\varpi }_{\lambda }={\varsigma }_{\lambda }^{\text{sca}}/{\varsigma }_{\lambda }^{\text{ext}}$
• scattering phase function properties; depending on the supported scattering mode this may be:
  • the assymmetry parameter $g$ for the Henyey-Greenstein phase function
  • a custom phase function ${\mathrm{\Phi }}_{\lambda }(\cos \theta )$ that depends only on the cosine of the scattering angle $\theta$
  • a custom phase function ${\mathrm{\Phi }}_{\lambda }(\theta ,\varphi )$ that depends on both scattering angles $\theta$ and $\varphi$, and on the polarization state of the incoming radiation
• the equilibrium temperature $T_{\text{eq}}$ for a given embedding radiation field, using average material properties and assuming local thermal equilibrium conditions

The DustMix class allows its subclasses to support the following scattering modes:

• HenyeyGreenstein: the subclass supplies the assymmetry parameter $g$ for the Henyey-Greenstein phase function. For a value of $g=0$, isotropic scattering is implemented directly rather than subsituting zero into the Henyey-Greenstein phase function.
• MaterialPhaseFunction: the subclass implements a custom phase function that depends only on the cosine of the scattering angle, $\cos \theta$. This mode does not support polarized radiation.
• SphericalPolarization: the subclass supports polarization through scattering by spherical particles. In this mode, the phase function depends on the polarization state of the incoming radiation, and the polarization state of the outgoing radiation must be updated appropriately. The phase function depends on both scattering angles $\theta$ and $\phi$.

The properties handled by the DustMix class correspond to the properties of a single grain population that is representative for the complete dust mix. In the context of tracking photon paths through a dusty medium, using properly calculated representive absorption and scattering cross sections and Mueller matrix coefficients is mathematically exact. In other words, for scattering modes MaterialPhaseFunction and SphericalPolarization, the representative grain approach does not involve an approximation. However, the calculation of a representative scattering asymmetry parameter $g$ for use with the HenyeyGreenstein scattering mode does involve a non-exact averaging procedure. Because the Henyey-Greenstein scattering phase function is non-physical to begin with, using a single approximate $g$ value for the complete dust mix is usually considered to be acceptable.

The DustMix class in turn has three abstract subclasses, each implementing a different approach to obtaining the relevant dust properties:

• SingleGrainDustMix implements a dust mix described by a single representative grain, with or without support for polarization by scattering. The optical dust properties are retrieved from stored table resources provided with SKIRT. For example, the MeanInterstellarDustMix class provides a basic model for interstellar dust that can be used in simulations that do not include thermal dust emission.
• TabulatedDustMix implements a dust mix described by tabulated properties for a single representative grain using the Henyey-Greenstein scattering mode. The optical dust properties are read from a user-supplied input file (MeanFileDustMix) or can be listed directly inside the parameter file (MeanListDustMix). These classes are provided mostly for testing and benchmarking purposes.
• MultiGrainDustMix implements a dust mix described by one or more grain populations, each with their own grain composition and size distribution, and with or without support for polarization by scattering. The class offers facilities to its subclasses to add dust grain populations to the dust mix. Based on this information it calculates the representative optical properties required for the common interface. See Multiple grain population dust mixes below.

Multiple grain population dust mixes

The information offered by the single representative dust grain classes is insufficient to accurately calculate dust emission spectra for the dust mixture. This is so because the emission spectrum is a nonlinear function of the grain size (among many other things), and thus a single grain cannot accurately represent a population with a potentialy large range of grain sizes. Furthermore, smaller dust grains are often not in local thermal equilibrium, and instead are heated stochastically by individual photon absorption events. Modeling emission for these grains involves a temperature probability distribution rather than just an equilibrium temperature. And lastly, the calculation obviously needs calorimetric properties of the grain material in addition to optical properties.

The MultiGrainDustMix class therefore implements additional functionality to allow calculating the emission spectrum for multiple grain populations with given optical and calorimetric properties and with a given size distribution. To enable these capabilities, the MultiGrainDustMix class obtains the following information for each of the dust grain populations added by the subclass: the absorption efficiencies $Q^{\text{abs}}(\lambda ,a)$, the scattering efficiencies $Q^{\text{sca}}(\lambda ,a)$, the scattering phase function asymmetry parameter $g(\lambda ,a)$, the Mueller matrix coefficients $S^{\text{xx}}(\lambda ,a,\theta )$, the bulk density ${\rho }_{\text{bulk}}$ of the grain material, and the properly normalized grain size distribution per hydrogen atom $\mathrm{\Omega }(a)=(\frac{\text{d}{n}_{\text{D}}}{\text{d}a})/n_{\text{H}}$ in the range $[a_{\text{min}},a_{\text{max}}]$.

The representative optical grain properties for use during the photon cycle are calculated from this information by integrating over the grain size distribution $\mathrm{\Omega }(a)$ and accumulating over all grain populations. See MultiGrainDustMix for details.

To calculate emission spectra, the class discretizes the grain size distribution for each type of grain material into a number of consecutive size bins, and calculates the optical and calorimetric properties of a representative grain for each of these bins. The number of bins for each type of grain material can be configured by the user. See MultiGrainDustMix for details.

The MultiGrainDustMix class uses one of two methods to calculate the emissivity of the dust mix:

• Assuming local thermal equilibrium for each representative grain (size bin): this method is fast but inaccurate because the equilibrium assumption is usually not justified. See the EquilibriumDustEmissionCalculator class for more information.
• Calculating a temperature probability distribution for each representative grain (size bin) to take into account stochastically heated grains: this second method is substantially more accurate but also much slower. See the StochasticDustEmissionCalculator class for more information.

Turn-key dust mixes

SKIRT offers a range of built-in "turn-key" dust mixes representing sets of dust properties that have been published by various authors, including for example:

• DraineLiDustMix: represents a dust mixture of silicate, graphite, and PAH dust grains designed by Draine & Li 2007 such that the global dust properties accurately reproduce the extinction curve of the Milky Way.
• ZubkoDustMix: represents a realistic dust mixture of bare silicate, graphite, neutral PAH and ionized PAH dust grains designed by Zubko, Dwek & Arendt 2004 such that the global dust properties accurately reproduce the extinction, emission and abundance constraints on the Milky Way.
• ThemisDustMix: represents the THEMIS model for dust in the diffuse interstellar medium described by Jones et al. 2017 and the references therein. The model includes amorphous silicates with forsterite-normative composition and with enstatite-normative composition, and amorphous carbonaceous dust grains.

Refer to the respective classes and to other DustMix subclasses for more information.

Configurable dust mixes

The ConfigurableDustMix class represents a fully user-configurable dust mix described by one or more dust grain populations. Specifically, the class can be configured with a list of GrainPopulation instances, each of which represents a particular dust grain population with configurable grain composition, grain size distribution, and size bin discretization. This is illustrated in the following diagram (connections starting with a triangle denote inheritance; connections starting with a diamond denote aggregation).

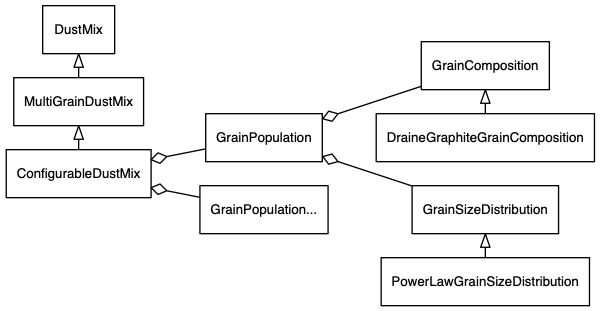
A GrainComposition object represents the optical and calorimetric properties of a particular grain material according to a certain model. A GrainSizeDistribution object represents a particular grain size distribution function. For each grain population, a ConfigurableDustMix object holds a GrainPopulation object, which in turn holds a GrainComposition object and a GrainSizeDistribution object, and specifies the number of size bins used for discretizing the size distribution.

In addition, the user can define the amount of dust in each grain population by specifying one of the following three quantities:

• an absolute dust mass per hydrogen atom;
• a ratio of dust mass per hydrogen mass;
• a proportionality factor on the size distribution.

For example, one could mimic an MRNDustMix with the following ski file configuration:

<ConfigurableDustMix scatteringType="HenyeyGreenstein">
    <populations type="GrainPopulation">
        <GrainPopulation numSizes="10" normalizationType="FactorOnSizeDistribution"
                         factorOnSizeDistribution="7.762471166e-31">
            <composition type="GrainComposition">
                <DraineSilicateGrainComposition/>
            </composition>
            <sizeDistribution type="GrainSizeDistribution">
                <PowerLawGrainSizeDistribution minSize="0.005 micron" maxSize="0.25 micron"
                                               exponent="3.5"/>
            </sizeDistribution>
        </GrainPopulation>
        <GrainPopulation numSizes="10" normalizationType="FactorOnSizeDistribution"
                         factorOnSizeDistribution="7.413102413e-31">
            <composition type="GrainComposition">
                <DraineGraphiteGrainComposition/>
            </composition>
            <sizeDistribution type="GrainSizeDistribution">
                <PowerLawGrainSizeDistribution minSize="0.005 micron" maxSize="0.25 micron"
                                               exponent="3.5"/>
            </sizeDistribution>
        </GrainPopulation>
    </populations>
</ConfigurableDustMix>

For more information and examples, see Configuring custom dust mixes.

Electrons

The ElectronMix class implements Compton scattering for a population of electrons, which converges to Thomson scattering at low photon energies. It is meaningful to implement both processes, because the calculations for Compton scattering are substantially slower than those for Thomson scattering.

Specifically, for wavelengths shorter than 10 nm, the class models Compton scattering, which features a wavelength-dependent cross section and phase function, and which causes the photon energy (wavelength) to change during the interaction. See the ComptonPhaseFunction class for more information. The current implementation of Compton scattering does not support polarization.

For wavelengths longer than 10nm, the scattering process can be described by elastic and wavelength-independent Thomson scattering. The scattering cross section is given by the well-known Thomson cross section (a constant) and the phase function is that of a dipole. See the DipolePhaseFunction class for more information. In this wavelength regime, polarization is fully supported (if enabled by the user).

It is also possible to request a random thermal motion to be added corresponding to the local kinetic temperature. See the ElectronMix class for more information.

Gas

There is no general implementation of gaseous media in SKIRT. Instead, each material mix class in this category implements one or more specific physical processes related to a given chemical species (atom, molecule, ion) or combination thereof. In this section, we merely summarize the capabilities of the classes available at the time of writing and refer to the individual class documentation for more information.

• The XRayAtomicGasMix class describes neutral atomic gas in the X-ray wavelength range, taking into account the effects of photo-absorption, fluorescence, and scattering by bound electrons. The class assumes a gas containing a mixture of non-ionized elements with atomic numbers from 1 (hydrogen) up to 30 (zinc). The spatial density distribution of the gas is established by setting the hydrogen density. The relative abundances of the 30 elements and the temperature of the gas can be configured by the user as spatially constant properties.
• The LyaNeutralHydrogenGasMix class describes Lyman-alpha resonant line transfer for a population of neutral hydrogen atoms, including support for polarization by scattering. The spatial distributions for both the density and the temperature of the neutral hydrogen gas must be defined by the input model and do not vary during the simulation.
• The SpinFlipHydrogenGasMix class describes the 21 cm spin-flip transition in neutral atomic hydrogen, including emission and absorption. The 21 cm emission luminosity and self-absorption opacity in a given cell are determined from gas properties defined in the input model (total hydrogen number density, neutral hydrogen mass fraction, gas metallity, gas temperature) and the local UV radiation field calculated by the simulation (taking into account dust extinction). The implementation includes a partitioning scheme to estimate the atomic and molecular fractions based on these input model properties and the radiation field.
• The NonLTELineGasMix class describes selected transitions in selected molecules and atoms. For each supported species (OH, HCO+, CO, C, C+), the current implementation includes a number of rotational energy levels (quantum number $J$) at the base vibrational level (quantum number $v=0$) for molecules and electronic energy levels and hyperfine split levels for atoms. The class performs an iterative, non-LTE calculation including the effects of collisional transitions (excitation and de-excitation with one or more types of interaction partners) and photonic transitions (spontaneous emission, absorption, and induced emission).

The SpinFlipHydrogenGasMix and NonLTELineGasMix classes inherit the EmittingGasMix class, which provides common functionality to gas mixes that support secondary emission. The XRayAtomicGasMix does not because fluorescence is implemented as a special form of scattering.