Spatial characteristics of the simulated model

In a SKIRT simulation, the spatial distributions of the model are defined as part of the SourceSystem (for the radiation sources) and the MediumSystem (for the transfer medium). The distributions may be specified through one or more of the built-in geometries (Geometry) or they may be imported from a snapshot generated by a hydrodynamical simulation.

In all cases, the spatial characteristics of the model are internally described in a three-dimensional, right-handed Cartesian coordinate system, with some provisions for keeping track of specific spherical or cylindrical symmetries where appropriate. In many cases the model domain is centered on the origin of the coordinate system, but this is not a requirement. In fact, facilities such as the OffsetGeometryDecorator class allow easily defining off-center structures.

A model is considered to be spherically or cylindrically symmetric if all sources and media components show the corresponding symmetry. By definition, a spherically symmetric model is centered on the origin, and a cylindrically symmetric model is centered on the vertical coordinate axis.

Spatial grids

A SKIRT simulation employs an instance of the SpatialGrid class to spatially discretize the transfer medium of the model. Properties such as the material density and the calculated radiation field are considered to be uniform within each cell of the grid. It is thus necessary to provide a sufficiently fine grid in the relevant areas of the model. On the other hand, simulation runtime and memory requirements scale with the number of cells, so it is often necessary to minimize the number of cells in less relevant areas of the model.

SKIRT offers a range of spatial grid options to help accomplish this balance. The following diagram shows the key classes in the SpatialGrid class hierarchy (connections starting with a triangle denote inheritance).

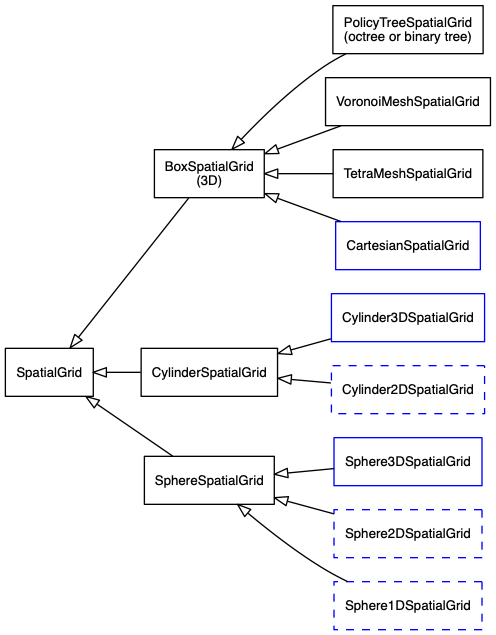
The PolicyTreeSpatialGrid class offers a spatial grid in which a cuboidal domain is recursively divided into two or eight subcells until the resulting cells meet some user-configured criteria, such as a maximum mass fraction or optical depth. This allows placing many small cells in relevant regions and fewer larger cells in other regions. This grid type is often used to handle density distributions that have a complex or unpredictable spatial structure.

The VoronoiMeshSpatialGrid class constructs a Voronoi tessellation to discretize the spatial domain; each cell is a convex polyhedron. Similarly, the TetraMeshSpatialGrid class uses tetrahedral cells. These grid types can be handy to mirror the discretization of an imported hydrodynamical snapshot. The CartesianSpatialGrid class uses regular grid spacing in each Cartesian coordinate direction. Each cell is a cuboid lined up with the Cartesian coordinate axes, although cells may have different sizes or form factors. This is a very fast grid useful for fairly smooth models.

The BoxSpatialGrid subclasses described above are defined in Cartesian coordinates and their configuration space is a cuboid lined up with the coordinate axes (often but not necessarily centered on the origin). On the other hand, the CylinderSpatialGrid subclasses are defined in cylindrical coordinates and their configuration space is a cylinder centered on the vertical coordinate axes. Likewise, the SphereSpatialGrid subclasses are defined in spherical coordinates and their configuration space is a sphere centered on the origin.

The BoxSpatialGrid subclasses can be used regardless of any symmetries in the model. This is also true for the Cylinder3DSpatialGrid and Sphere3DSpatialGrid classes, although these are more beneficial for models with a corresponding approximate symmetry, so that some of the cell borders are more or less lined up with equidensity surfaces in the model.

The Cylinder2DSpatialGrid class provides spatial grids defined in the meridional $(R, z)$ plane and rotated around the vertical coordinate axis. Similarly, the Sphere2DSpatialGrid class provides spatial grids defined in the meridional $(r, θ)$ plane and rotated around the vertical coordinate axis. These grids can be used only for axisymmetric models defined with built-in geometries. Finally, the Sphere1DSpatialGrid class provides spatial grids in which the grid cells are concentric shells. It can be used only when the model is spherically symmetric. Because of the reduced dimensionality, these 1D or 2D grids (indicated in the diagram with a dashed border) perform significantly faster than their 3D counterparts, making them the preferred choice for models with the relevant symmetries.

The classes indicated in the diagram with a blue border (solid or dashed) implement regular spatial grids. These grid types require the user to define the position of the cell borders in each coordinate dimension through Mesh subclass instances, as described in the next section.

Meshes

LinMesh (horizontal) and SymPowMesh (vertical)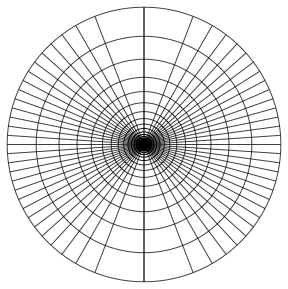

LogMesh (radial) and SymCosMesh (polar)

In SKIRT, an instance of a Mesh subclass characterizes a one-dimensional mesh over the unit interval $[0, 1]$ . A mesh is essentially a partition of this interval into $N$ bins defined by an ordered sequence of $N + 1$ mesh points $t_{i}$ with $t_{0} = 0$ and $t_{N} = 1$ . A SpatialGrid subclass instance using a Mesh instance is responsible for applying a linear transform from the unit interval $[0, 1]$ on which the mesh is defined to the range of the spatial domain in the applicable coordinate direction.

The following list briefly describes the key Mesh subclasses offered by SKIRT.

LinMesh has equidistant (linearly distributed) mesh points.
PowMesh has a power-law distribution of the mesh points. The bin sizes form a geometric series, i.e. each bin is a constant factor larger than the previous one. The distribution is characterized by a single user-configurable parameter, the bin width ratio between the last and the first bin.
LogMesh has a logarithmic distribution of the mesh points. The first bin covers a user-configurable fraction of the unit interval, and the widths of the other bins are distributed logarithmically over the remaining portion of the interval.
SymPowMesh has a symmetric power-law distribution of the mesh points. The bin sizes form a geometric series starting from the innermost bin and moving outwards symmetrically. If the number of bins is odd, there is one innermost bin; if it is even, there are two equal-size innermost bins.
SymLogMesh has a symmetric logarithmic distribution of mesh points mirrored around the center. If the number of bins is odd, there is one innermost bin with user-configurable width; if it is even, there are two equal-size innermost bins.
SymCosMesh has its mesh points distributed such that when the mesh is used to subdivide a spherical volume into conical slices by polar inclination angle $0 \leq θ \leq π$ , the resulting slices have equal volume.
FileMesh and ListMesh allow the user to configure any desired set of custom mesh points.

Any of these Mesh subclass instances can be used to define the grid points for any coordinate direction in any regular spatial grid. In certain contexts, some are more useful than others though. For example, SymPowMesh and SymLogMesh are often handy to discretize a Cartesian coordinate axis that crosses the origin, while they seem less applicable to a radial coordinate axis. Also, the SymCosMesh class is mostly intended for discretizing the polar $θ$ coordinate axis.